
| Naslain.com |
Come and see a new dive site guide, Wannadive.net. Don't hesitate to contribute by adding your favourite dive sites.
Wannadive.net
|
|
|
|

 Print Print
 Send Send
|
|
|
| Domeport, flatport, How do they works ? |
| Author : Christophe Naslain / Date : 20/01/2003 |
L'objectif de cet article est de comprendre ce qui se passe quand on utilise un hublot
sphérique (dôme) ou un hublot plan en photographie sous-marine.
La limite de l'utilisation des hublots plans dérive directement des phénomènes de réfraction de la lumière sur la surface
de ces hublots. Quand on utilise un hublot plan, plusieurs problèmes vont se poser lorseque la focale de l'objectif diminue et se
trouve inférieure à 28 mm (cas des objectifs grand-anglulaires) :
- Limitation de l'angle de champ
- Distorsion
- Aberration chromatique
 Limitation de l'angle de champ : Rappelons tout d'abord ce qu'est la réfraction d'un rayon lumineux et la loi de
Snell-Descartes. La réfraction est le changement de direction que subit un rayon lumineux quand il passe d'un milieu
transparent à un autre milieu transparent. Dans le cas d'un hublot, deux changements vont se produire : eau / verre et verre / air.
Ce phénomène est provoqué par le changement de la vitesse de propagation de la lumière à travers ces milieux. Le rapport des
ces vitesses est appelé l'indice de réfraction, noté n. Nous aurons besoin pour ce qui suit de connaître les
indices de réfraction de l'eau ( n=1.33 ) du verre ( n=1.52 ) et de l'air ( n=1 ).
Limitation de l'angle de champ : Rappelons tout d'abord ce qu'est la réfraction d'un rayon lumineux et la loi de
Snell-Descartes. La réfraction est le changement de direction que subit un rayon lumineux quand il passe d'un milieu
transparent à un autre milieu transparent. Dans le cas d'un hublot, deux changements vont se produire : eau / verre et verre / air.
Ce phénomène est provoqué par le changement de la vitesse de propagation de la lumière à travers ces milieux. Le rapport des
ces vitesses est appelé l'indice de réfraction, noté n. Nous aurons besoin pour ce qui suit de connaître les
indices de réfraction de l'eau ( n=1.33 ) du verre ( n=1.52 ) et de l'air ( n=1 ).
Le comportement des rayons lumineux est décrit par les lois de Snell-Descartes, dont :
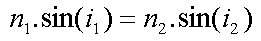
Voici le schéma de deux rayons lumineux :
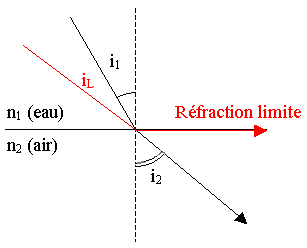
Prenons l'eau comme milieu 1 et l'air comme milieu 2. On négligera le passage dans le verre en considérant que le
hublot est à faces parallèles. Que peut-on tirer de cette loi ?
- Un rayon lumineux qui tombe perpendiculairement à la surface du hublot ne sera pas dévié : i1
= 0° => sin(0°) = 0 => i2 = 0.
- Comme l'air est moins réfringent que l'eau, n2 < n1, alors i2 > i1 : en
traversant le hublot, les rayons lumineux s'éloigneront de la normale.
- Si l'angle i1 est tel que l'on ait : n1 sin(i1) > 1, alors il n'y a plus de rayon réfracté. La
lumière ne sort plus de l'eau mais est complètement réfléchie, comme sur un miroir : on parle de réflexion totale. Cela
se produit quand le rayon incident est supérieur à 48°35' car iL = arcsin( nair/ neau
) = 48,59° = 48°35'.
Ce dernier point nous intéresse tout particulièrement dans le cas de notre hublot plan. En effet, si un rayon lumineux arrive avec
un angle supérieur à 48°35', il ne pénètrera pas dans le hublot et sera complètement réfléchi. En multipliant cet angle par deux,
on obtient l'angle de champ maximum qui peut être utilisé dans un hublot plan soit environ 97°. Sans aller jusque là,
un objectif de 90° d'angle correspond à une focale de 20 mm. On ne peut donc utiliser de grand-angles de focale
inférieure à 20 mm avec un hublot plat.
 La distorsion : Cette aberration est due aux phénomènes de réfraction sur le hublot plan. On considère
qu'en moyenne, le grossissement dans l'eau est de 4/3. Ceci n'est pas tout à fait exact. Dès qu'on s'écarte
de l'axe optique, le grossissement croit et ceci de façon non linéaire. Le grossissement sur les côtés étant plus important.
Il en résulte une distorsion "en coussinet". Cette aberration est pratiquement négligeable avec des objectifs de
longue et moyenne focale. En revanche, elle est visible avec des grand-angles. Un moyen de mettre en évidence cette
distorsion est de photographier les carreaux d'une piscine. Voici en exagérant ce que cela pourrait donner :
La distorsion : Cette aberration est due aux phénomènes de réfraction sur le hublot plan. On considère
qu'en moyenne, le grossissement dans l'eau est de 4/3. Ceci n'est pas tout à fait exact. Dès qu'on s'écarte
de l'axe optique, le grossissement croit et ceci de façon non linéaire. Le grossissement sur les côtés étant plus important.
Il en résulte une distorsion "en coussinet". Cette aberration est pratiquement négligeable avec des objectifs de
longue et moyenne focale. En revanche, elle est visible avec des grand-angles. Un moyen de mettre en évidence cette
distorsion est de photographier les carreaux d'une piscine. Voici en exagérant ce que cela pourrait donner :
 |
|
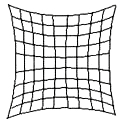 |
| Objet Normal |
|
Coussinet |
 L'aberration chromatique : Cette aberration est due au fait que l'indice de réfraction d'un milieu est
fonction de la longueur d'onde de la lumière qui la traverse. Cette aberration chromatique sera d'autant plus importante
que les rayons arriveront sur l'objectif avec un angle important. Ce cas se produit quand on utilise un grand-angle.
Le résultat est observable à la périphérie des images obtenues ; on peut y observer de fines franges colorées.
L'aberration chromatique : Cette aberration est due au fait que l'indice de réfraction d'un milieu est
fonction de la longueur d'onde de la lumière qui la traverse. Cette aberration chromatique sera d'autant plus importante
que les rayons arriveront sur l'objectif avec un angle important. Ce cas se produit quand on utilise un grand-angle.
Le résultat est observable à la périphérie des images obtenues ; on peut y observer de fines franges colorées.
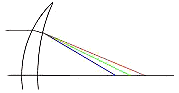
Schéma : L'aberration chromatique.
Les objectifs actuels sont calculés pour éviter ce défaut optique (lentilles achromatiques et apo-chromatiques). Le problème du
hublot plan vient du fait que son verre n'est pas compensé. Il génère donc une aberration chromatique.
(Plus d'infos... Les aberrations et les
défauts des lentilles. Lire le fichier PDF disponible en haut de page).
 Pour éliminer ces problèmes de réfraction, une solution est d'utiliser un hublot sphérique. L'idée fondamentale est que les
rayons qui convergent vers son centre, selon une incidence verticale, ne sont pas réfractés. La réfraction et les aberrations de
distorsions et chromatiques sont ainsi fortement réduites, voir annulées.
Pour éliminer ces problèmes de réfraction, une solution est d'utiliser un hublot sphérique. L'idée fondamentale est que les
rayons qui convergent vers son centre, selon une incidence verticale, ne sont pas réfractés. La réfraction et les aberrations de
distorsions et chromatiques sont ainsi fortement réduites, voir annulées.

Photo : Dôme sphérique Subal.
Le hublot sphérique est dans le jargon opticien ce que l'on appelle un dioptre sphérique (un dioptre est l'interface entre
deux milieux transparents homogènes d'indices optiques différents). Placé dans un milieu aquatique, ce dioptre génère une image
virtuelle. Il se comporte comme un lentille divergente de forte puissance. Voici un schéma optique de ce système :
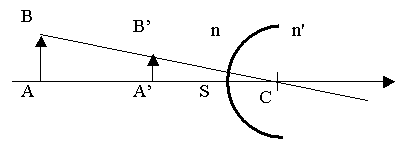 Avec :
Avec :
- AB : le sujet photographié,
- A'B' : l'image virtuelle générée,
- C : le centre du dioptre,
- S : la surface du dioptre (S est l'origine des distances),
- n : l'indice de réfraction de l'eau,
- n' : l'indice de réfraction de l'air.
L'utilisation de la relation de Conjugaison du dioptre sphérique permet de déterminer la position de
cette image virtuelle.
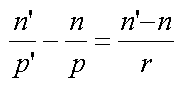 Avec :
Avec :
- p = SA, la distance du sujet
- p' = SA', la distance de l'image virtuelle,
- n : l'indice de réfraction de l'eau,
- n' : l'indice de réfraction de l'air.
- r : le rayon de courbure du dioptre.
On tire de cette relation p', la distance de l'image virtuelle qui est donnée par rapport à la surface
du dioptre :
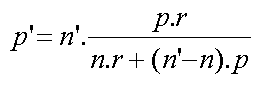 Au niveau de l'appareil photo, tout se passe comme si on prenait en photo cette image virtuelle. La mise au point
sera donc faite sur cette image virtuelle.
Au niveau de l'appareil photo, tout se passe comme si on prenait en photo cette image virtuelle. La mise au point
sera donc faite sur cette image virtuelle.
Le grandissement (ou rapport de grandeur) est calculé grâce à la formule suivante :
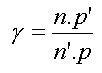 Prenons un hublot sphérique de 20 cm de rayon et calculons la position et la grandissement de l'image virtuelle :
Prenons un hublot sphérique de 20 cm de rayon et calculons la position et la grandissement de l'image virtuelle :
| Distance de l'objet (m) |
Distance de l'image virtuelle (m) |
Grandissement |
| Infini |
-0.60 |
0 |
| -2 |
-0.43 |
0.29 |
| -1.5 |
-0.39 |
0.35 |
| -1 |
-0.33 |
0.44 |
| -0.5 |
-0.23 |
0.62 |
| -0.3 |
-0.16 |
0.73 |
| -0.15 |
-0.09 |
0.84 |
Attention : Les distances sont des distances scalaires. Le point de référence
étant le point S, les distances de l'objet et de l'image virtuelle sont donc bien négatives.
On observe que l'image virtuelle générée par le dioptre est toujours plus proche que l'image réelle. Pour un
objet situé à l'infini, cette distance est de :
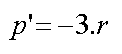
Soit pour notre exemple de hublot de 20 cm de rayon, 20 cm x 3 = 60 cm. En imaginant des photos sont prises entre l'infini
et 30 cm, cela signifie que la plage de mise au point de notre objectif ira de 0.33 à 0.80 m !
Le grandissement est toujours inférieur à 1, ce qui signifie que l'image obtenue est toujours plus petite que l'image réelle.
Notons également que plus l'image est proche et moins le grandissement diminue.
 Qu'en est-il du positionnement de l'objectif par rapport au dioptre ? Est-ce important ?
Qu'en est-il du positionnement de l'objectif par rapport au dioptre ? Est-ce important ?
Optiquement, il n'y a pas de règle qui impose une certaine distance entre le hublot et l'objectif. Quelque soit la position de
l'objectif derrière le hublot sphérique, l'image virtuelle sera toujours à la même position par rapport au dioptre. Une
contrainte à prendre en compte est la distance minimum de mise au point de l'objectif. En effet, si l'image virtuelle est
trop proche, l'appareil ne pourra faire la mise au point...
Cependant, étant donné que les rayons normaux au hublot arrivant au centre de la sphère ne sont pas réfractés, il
est préférable de placer le centre optique de l'objectif au centre de la sphère. Ainsi, l'angle de champ
de l'objectif n'en sera pas modifié et les phénomènes de distorsion seront éliminés. C'est pour cela que l'on est parfois contraint
d'utiliser une bague allonge pour éloigner le dôme de l'objectif. Un objectif de 17 mm à l'air restera un 17 mm sous
l'eau.
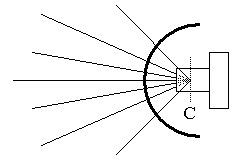
Schéma : Positionnement du centre optique de l'objectif au centre du dioptre.
 A noter également que le hublot plan, qui est utilisé pour les objectifs de focale supérieures à 28 mm, est en fait
un cas particulier de la relation de conjugaison du dioptre sphérique. Dans ce cas précis, le rayon de courbure est infini.
La relation de conjugaison du dioptre plan est donc la suivante :
A noter également que le hublot plan, qui est utilisé pour les objectifs de focale supérieures à 28 mm, est en fait
un cas particulier de la relation de conjugaison du dioptre sphérique. Dans ce cas précis, le rayon de courbure est infini.
La relation de conjugaison du dioptre plan est donc la suivante :
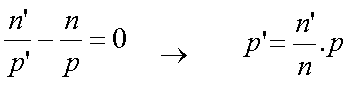
D'ou pour notre hublot plan dans l'eau : p' = 3/4.p. On retrouve notre bon vieux principe qui dit que dans l'eau, les
objets paraissent plus proches, leur image située à 3/4 de la distance de l'objet. Qu'en est-il du grandissement ?
Tout le monde sait bien que dans l'eau les objets paraissent plus grands... mais est-ce vrai ? Reprenons la formule du
grandissement du dioptre sphérique et remplaçons p' par sa valeur. Nous obtenons ceci :
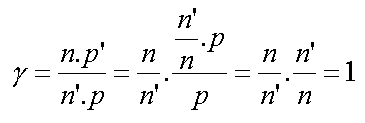
... et bien non ! Dans le cas d'un dioptre plan l'image virtuelle a la même taille que l'objet ! Le fait que l'image virtuelle soit
plus proche fait qu'on la perçoit plus grande. Pour expliquer cela, imaginez que vous regardez un objet avec un angle de champ défini.
En rapprochant l'objet, sa taille ne change pas. Mais en conservant le même angle de champ, vous ne verrez qu'une partie de cet
objet. Il vous semblera qu'il a grossi.
 Remerciements : Remerciements :
- Bruno Bousquet, Maître de conférence au CPMOH,
pour ses calculs, ses explications et conseils avisées en optique.
- Luc Penin, Photographe sous-marin, pour ses commentaires et suggestions sur la première version de cet article.
|
|
|
Comments |
 Add a comment
Add a comment
| Comment from Béatrice Romain
|
| Ca y est, j'ai enfin compris comment mon bon vieux hublot marchais. Je trouve cet article vraiement bien fait et malgrès ces formules un peu barbares, c'est très clair. |
| Posted date 6/02/2003 |
|
| Comment from Bernard
|
Alors là pour une fois voilà une explication compréhensible!
J'ai tout lu sauf les formules ...
Mais qu'en est-il des aberrations introduites par le dôme et la bonnette 4D ajoutée pour permettre la mise au point?
Le remède ne serait-il pas pire que le mal pour un objectif de 24 ou 28mm?
|
| Posted date 13/04/2003 |
|
| Comment from Laurent
|
Bonjour,
Ou trouver un hublot sphérique pour équiper mon bon vieux caisson vidéo ??
Merci d'avance |
| Posted date 19/02/2006 |
|
|
|
 Print Print
 Send Send
|
|
|
