 L'indice de réfraction L'indice de réfraction
 La réflexion totale La réflexion totale
 Les distances et taille apparentes Les distances et taille apparentes
 La distance focale La distance focale
 Le rapport de grandeur Le rapport de grandeur
 La tolérance de netteté La tolérance de netteté
 Le numéro de diaphragme Le numéro de diaphragme
 Profondeur de champ Profondeur de champ
 La tolérance de netteté La tolérance de netteté
 Distance hyperfocale Distance hyperfocale
 Premier plan net Premier plan net
 Dernier plan net Dernier plan net
 Profondeur de champ Profondeur de champ
 Macro - Tube allonge Macro - Tube allonge
 Macro - Numéro de diaphragme reel Macro - Numéro de diaphragme reel
Chaque fois que la lumière change de milieu, elle subit une déviation de
sa direction originale. C'est la réfraction. L'exemple le plus connu est le baton plongé
dans l'eau. Il apparait cassé. Ce phénomène provient des différences d'indices de
réfraction (n) de chaque milieu.
nair = 1
neau = 1,33 |
n : Indice de réfraction |
En réalité l'indice de référence est le vide, son indice est 1. Comme
l'indice de l'air est très proche de celui du vide : 1,0002926 on l'assimile à 1. Pour
information, l'indice de réfraction décrit également le rapport entre la vitesse de la
lumière dans le vide et celle du milieu considéré. On peut ainsi déterminer la vitesse
de la lumière dans l'eau :
Veau = Vair / Indiceeau = 300 000 /
1,33 = 225 563 Km/Seconde
Un autre phénomène intéressant en photographie sous-marine est la
réflexion totale. Ce phénomène fait que dans l'eau, si on regarde la surface sous un
certain angle (l'angle de réfraction limite), la surface de l'eau se comporte comme un
mirroir. L'angle de réfraction limite se calcule avec la formule de la réfraction :
n.Sin(i) = n'.Sin(i').
Angle Réfraction Limite : Sin (i') = Sin (90°) / 1,33 = 1 / 1,33 =
0,7518 d'où i' = 48° 75'
En photographie sous marine, on est constamment sous l'influence de la
réfraction. Le trajet de la lumière dans l'appareil photo se fait dans l'air tandis que
le le trajet de la lumière entre le sujet et l'objectif se fait dans l'eau. Pour les
calculs de distances, on fera une approximation supplémentaire en négligeant la partie
aèrienne entre la lentille et le dome ou l'extrémité de l'objectif.
Sous l'eau, les objets semplent plus près et plus gros que dans l'air.
Pour calculer la distance apparente et la taille apparente, on appliquera les relations
suivantes :
Distapp = DistRéelle / neau
Tailleapp = TailleRéelle x neau |
n : Indice de réfraction |
Un objectif photo est caractérisé par sa focale et son ouverture.
L'objectif est constitué d'un ensemble de lentilles de verre, assemblées en groupe de
lentilles. Pour simplifier et calculer les caractéristiques d'un objectif photo, on
assimilera l'objectif à une lentille simple.
Une lentille est carractérisée par son centre optique C, origine de
toutes les distances, et par ses foyers F et F'. Les deux foyers sont equidistants et se
trouvent de part et d'autre du centre optique. Le foyer est le point où se rencontrent
les rayons qui proviennent de l'infini et qui sont parallèles à l'axe optique. La
distance qui sépare le centre optique du foyer est appellé focale, notée f.
Le rapport de grandeur est le rapport entre la taille de l'image et la
taille de l'objet photographié. On le désigne par le symbole m. Il est également égal
au rapport entre le tirage et la distance de prise de vue.
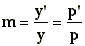 |
m : Rapport de grandeur
y' : Taille de l'image ( m )
y : Taille de l'objet ( m )
p' : Tirage de l'objectif ( m )
p : Distance de prise de vue ( m ) |
Dans le cas de la macrophotographie, on carractérisera les tubes allonges
par le rapport de grandeur. Par exemple chez Nikon, on trouvera 3 taille de tubes : 1:2 (m
= 0,5), 1:1 (m = 1) et 2:1 (m = 2).
Exemple : Si on veut photographier une limace de 50 mm sur un film
24x36 en hauteur, et que la limace remplisse le champ du film, il faudra un système de m
= 36 / 50 = 0,72.
Les diaphragmes actuels sont dits à iris. Ils sont composés de lamelles
métalliques, noircies et matées pour éviter les réflexions. Les numéros de
diaphragmes ( k ) correspond au rapport entre la focale ( f' ) et le diamètre du
diaphragme ( d ) :
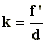 |
k : Numéro de diaphragme
f' : Focale de l'objectif ( mm )
d = Diamètre du diaphragme ( mm ) |
Les numéros de diaphragmes ont été fixés selon l'échelle
internationale suivante, en une progression géométrique de raison √ 2 soit 1,414 :
1 - 1,4 - 2 - 2,8 - 4 - 5,6 - 8 - 11 - 16 - 22 - 32 etc.
Lorseque l'on passe à un numéro immédiatement supérieur ou inférieur
de cette échelle, le temps de pose double ou devient moitié de ce qu'il était.
Le mécanisme de l'iris par chevauchement de lamelle fait qui'il est
possible de positionner le diaphragme entre deux numéros de diaphragme. C'est ainsi que
des objectifs affichent une ouverture de 3,5.
Les temps de pause sont directement proportionnels aux numéros de diaphragme. Exemple :
| Temps de pause : |
N° de diaphragme : |
| 1/1000 |
1,4 |
| 1/500 |
2 |
| 1/250 |
2,8 |
| 1/125 |
4 |
| 1/60 |
5,6 |
| 1/30 |
8 |
| 1/15 |
11 |
| 1/8 |
16 |
| 1/4 |
22 |
| 1/2 |
32 |
| 1 |
45 |
| 2 |
64 |
Les temps de pause sont en général notés 250, 125, 60 etc au lieu de 1/250, 1/125,
1/60 etc. On constate donc que plus le diaphragme est fermé (n° de diaphragme grand), et
plus le temps de pause est long. Ceci est logique puisque en fermant le diaphragme, on
limite la quantité de lumière sur le film. Il faut donc augmenter le temps de pause pour
bien exposer le film.
Si l'on souhaite déterminer le temps de pause pour un numéro de diaphragme qui ne
fait pas partie de l'échelle internationale, on appliquera la relation suivante :
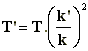 |
T : Temps de pause recherché ( s )
T : Temps de pause à k ( s )
k : numéro de diaphragme
k : Nouveau numéro de diaphragme |
Exemple : 1/15 ème à 2. Temps da pause à 20 ? T = (1/15) . (20 /
2)2 = 6,66 secondes.
La tolérance de netteté est la limite entre ce qui est net et ce qui est
flou. Lorsequ'un point ou un trait dépasse 1/10 ème de mm, notre oeil le voit flou.Un
point-objet n'est pas un point-image mais une tache image appellée cercle de diffusion.
La tolérance de netteté (u) des négatifs est variable selon les
individus. Des valeurs ont été fixées :
- 1/30 ème de mm pour le format 24x36
- 1/20 ème pour les 6x6 et les 6x9
- 1/10 ème pour les formats 9x12 et supérieurs
La distance hyperfocale (h) est la distance de l'avant-plan encore nette, à un certain
numéro de diaphragme, lorseque la mise au point est faite sur l'infini.
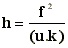 |
h : distance hyperfocale ( mm )
f : focale de l'objectif ( mm )
u : tolérance de netteté ( mm )
k : numéro de diaphragme |
Exemple : Objectif de 35 mm, diaphragme 8 et 3 mètres : h = 35 2 / (
0,03 . 8 ) = 4 593 mm = 4,59 m.
La distance hyperfocale n'est pas très utilisée en photographie sous marine car ces
distances sont bien souvent trop éloignées pour la porte des flashs sous-marins. On
pourrait utliser cette distance pour les photos d'ambiance, sans flashs. Le règlage à
faire serait alors de positionner la bague des distances sur la distance hyperfocale. La
zone de netteté s'étendrait alors de la moitié de la distance hyperfocale jusqu'à
l'infini.
C'est la distance qui sépare l'avant-plan net du centre optique de l'objectif (disons
l'objectif).
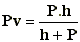 |
Pv : Premier plan net ( m )
P : Distance de prise de vue ( m )
h : Distance Hyperfocale ( m ) |
C'est la distance qui sépare l'arrière-plan net du centre optique de l'objectif.
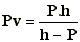 |
Pv : Premier plan net ( m )
P : Distance de prise de vue ( m )
h : Distance Hyperfocale ( m ) |
NB : Si ( h - P ) devient négatif, on admet qu'il s'agit de l'infini.
La profondeur de champ (pc) peut être définie comme étant une zone de netteté
qui s'étand de l'avant-plan net du sujet (Premier plan net, ppn), passe par le plan de
mise au point et finit à l'arrière plan net (Dernier plan net, dpn).
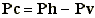 |
pc : Profondeur de champ ( m )
Ph : Dernier plan net ( m )
Pv : Premier plan net ( m ) |
Un tube allonge est un tube (sans aucune lentille) qui se place entre le boîtier et
l'objectif pour en augmenter le tirage, et ainsi permettre des grandissements supérieurs.
- Pour un mise au point réglée sur l'infini :
Le grandissement est déterminé comme suit :
|
Ginfini = Tb / f |
G : Grandissement
Tb : Tirage de la bague ( mm )
f : Focale de l'objectif ( mm ) |
La distance de mise au point réelle est déterminé comme suit :
|
Dréelle = ( 1 + 1 / Ginfini ) . f |
D : Distance réelle ( mm )
G : Grandissement
f : Focale de l'objectif ( mm ) |
- Pour un mise au point différente, on tient compte du tirage de l'objectif :
Tirage de l'objectif à la distance de mise au point :
|
Tobj = ( Dmap . f ) / (Dmap - f ) |
Tobj : Tirage de l'objectif (mm)
Dmap : Distance de mise au point ( mm )
f : Focale de l'objectif ( mm ) |
Le tirage total de l'objectif et du tube allonge est :
|
Ttot = Tobj + Ttube |
Ttot : Tirage de l'ensemble (mm)
Tobj : Tirage de l'objectif (mm)
Ttube : Tirage du tube (mm) |
Le grandissement est déterminé comme suit :
|
Gmap = ( Ttot - f ) / f |
G : Grandissement
Ttot : Tirage de l'ensemble (mm)
f : Focale de l'objectif ( mm ) |
La distance de mise au point réelle est alors :
|
Dréelle = ( 1 + 1 / Gmap ) . f |
D : Distance réelle ( mm )
G : Grandissement
f : Focale de l'objectif ( mm ) |
Les numéros de diaphragme qui sont inscrits sur les objectifs ont été déterminés
en fonction du diamètre du diaphragme et de la focale de l'objectif (voir diaphragme). Si on utilise un tube allonge, on va modifier le
tirage de l'ensemble (Tube + Objectif). Les numéros de diaphragme doivent donc être
recalculés.
|
k Obj+Tube = Ttot / ( f / k ) |
k Obj+Tube : No de diaphragme
Ttot : Tirage de l'ensemble (mm)
f : Focale de l'objectif ( mm )
k : numéro de diaphragme (Obj) |
| 